Decision making in venture capital relies heavily on probabilistic thinking and difficult-to-compare historical data. The heuristics are too rough and the feedback loops are too long. Most of the time correlation does not imply causation. You can’t distinguish “A causes B,” “B causes A,” and “C causes both A and B.”
You can get around the correlations vs causation problem by treating startup success as a function of independent variables (see Leo Polovets’ great post on this). Since most investors assess risk through empirical data and qualitative measures learned through pattern recognition, human biases can easily influence decision making.
Here’s my favorite example which is pulled from Michael Nielsen’s excellent post:
Suppose you’re suffering from kidney stones and go to see your doctor. The doctor tells you two treatments are available, treatment A and treatment B. You ask which treatment works better, and the doctor says “Well, a study found that treatment A has a higher probability of success than treatment B.”
You start to say “I’ll take treatment A, thanks!”, when your doctor interrupts: “But the same study also looked to see which treatment worked better, depending on whether patients had large kidney stones or small kidney stones.” You say “Well, do I have large kidney stones or small kidney stones”? As you speak the doctor interrupts again, looking sheepish, and says “Actually, it doesn’t matter. You see, they found that treatment B has a higher probability of success than treatment A, regardless of whether you have large or small kidney stones.”
Take a second to wonder: how is that possible? I was initially stumped, and a couple brilliant friends of mine couldn’t think of a concrete explanation off the top of their heads. It turns out that this result came from a legitimate real-life study. The sample sizes of the different groups were not controlled:
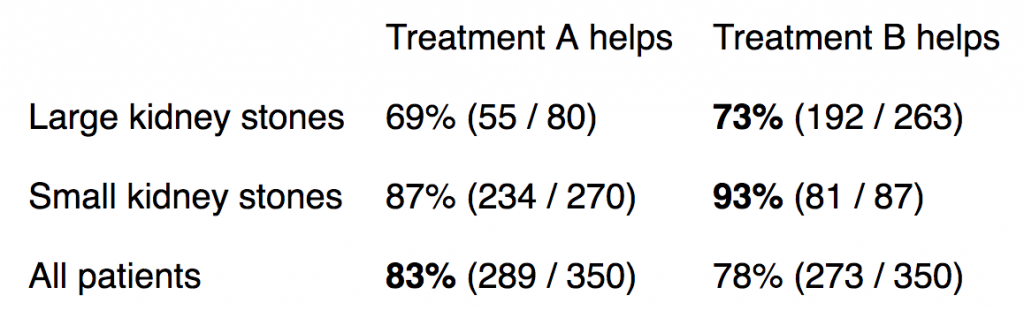
Okay, that makes sense. But the point is that empiricism can easily fail when you treat complex problems as a set of independent variables.
VC is pretty famous for fitting power law distributions and having skewed samples sizes. Replacing large/small kidney stones with a startup-relevant category and Treatment A/B with something a startup is doing, you’ll have a massively uneven set of data points to draw in — this is precisely what opens the door to Simpson’s Paradox.
The question then becomes: what are the most important cases of Simpson’s Paradox in VC? Perhaps large founding teams, or “distracted teams” consisting of university professors fit the bill. There are few examples of this, especially compared to the number of standard 2-3 cofounders we’re used to, so the statistical waters are muddied.
Tomasz Tunguz wrote that this type of thinking can also be applied to finding market opportunities: (In 2013 no less — ahead of the game!)
The Berkeley example reminds me of the SpaceX’s formation story Elon Musk shared at the D conference this year. Musk implicitly knew launching satellites into space would be expensive. After all, NASA’s annual budget is about $19B. But when Musk and his team analyzed each cost component of a space launch, they found that less than 10% of the costs were the rocket and the fuel and the launch equipment. This meant Musk could conceivably reduce the costs of space shipping by 80%.
While it’s not a true statistical example of Simpson’s Paradox, the point is the same. The market held a worldview based on aggregate data. But Musk recognized the aggregate space costs didn’t tell the true story. By digging deeper, he and his team found a lurking explanatory variable and an opportunity to disrupt the industry.
I think everyone should read about the common statistical paradoxes and fallacies. An obvious followup post would cover something like Bayes’ Rule in VC. Only one in five doctors correctly answer the linked Probability 101 question related to cancer rates (!!!) and I bet this many investors fall into similar traps.